Cartesian Coordinates
These are regular coordinates, x coordinates go in and out, y-coordinates go left and right, and z coordinates go up and down.
Cylindrical Coordinates
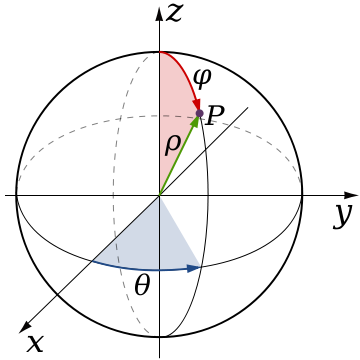
Spherical Coordinates
Points are usually written as: ($\rho$, $\theta$, $\phi$). Note, some textbooks, like Swokowski, use ($\rho$, $\phi$, $\theta$).
Converting between Cartesian and Cylindrical
Cartesian to Cylindrical
First, we have to remember that the z stays the same, so we only have to focus on the xy-plane.
r is just the radius of the circle, and $x^2 + y^2 = r^2$, so r = $sqrt(x^2 + y^2)$.
Now, we are left with finding $\theta$. We have three equations to use for this:
$$x = r\cos(\theta), y = r\sin(\theta)\text{, and }\frac{y}{x} = \tan(\theta)$$
Whichever one you choose, you get two possible thetas. Once you find your possible thetas, you have to substitute it back in for x and y to see if it works.
$$(r,\theta,z) = \begin{cases}
r = \sqrt{x^2 + y^2}\\
\theta = \arctan\left(\dfrac{y}{x}\right)\\
z = z
\end{cases}$$
Cylindrical to Cartesian
Once again, z stays the same, so we have to go from r and $\theta$ to x and y.
So, x = $r\cos(\theta)$, and y = $r\sin(\theta)$. That's it.
$$(x,y,z) = \begin{cases}
x = r\cos(\theta) \\
y = r\sin(\theta) \\
z = z
\end{cases}$$
Converting between Cartesian and Spherical
Cartesian to Spherical
The first thing we can do find $\rho$. That's the radius of the sphere, and it equals $x^2 + y^2 + z^2$. Now, we can make two triangles. $z = \rho\cos(\phi) \rightarrow \phi = \arccos\left(\dfrac{z}{\rho}\right)$
We can do the same thing with the bottom triangle. $\dfrac{y}{x} = \tan(\theta) \rightarrow \theta = \arctan\left(\dfrac{y}{x}\right)$
Once again, you should plot the points to make sure the theta works.
$$(\rho, \theta,\phi) = \begin{cases}
\rho = \sqrt{x^2 + y^2 + z^2} \\
\theta = \arctan\left(\dfrac{y}{x})\right) \\
\phi = \arccos\left(\dfrac{z}{\rho}\right)
\end{cases}$$
I changed some stuff, so that's why a few of the variables look bad.
Spherical to Cartesian
The first thing we could look at is the top triangle. $\phi$ = the angle in the top right of the triangle. So $\rho\cos(\phi) = z$
Now, we have to look at the bottom triangle to get x and y.
In order to do that, though, we have to get r, which equals $ \rho\sin(\phi)$. Now, y = $r\sin(\theta)$ = $\rho\sin(\phi)\sin(\theta)$. Note that even if $\theta > \frac{\pi}{2}$, that works, because we can just think of it by using the circle definition of trig, by eliminating the z, or flattening the graph. Same with y, $x = r\cos(\theta) = \rho\sin(\phi)\cos(\theta)$.
$$(x,y,z) = \begin{cases}
x = \rho\sin(\phi)\cos(\theta) \\
y = \rho\sin(\phi)\sin(\theta) \\
z = \rho\cos(\phi)
\end{cases}$$
Converting between Cylindrical and Spherical
Cylindrical to Spherical
Cylindrical and spherical both share a $\theta$, so we don't have to worry about that. Now, we have to find the $\rho$ and the $\phi$. So, we can note this triangle.
$$\rho^2 = r^2 + z^2$$
Looking at the top triangle, we can say
$$\tan(\phi) = \dfrac{r}{z} \rightarrow \phi = \arctan\left(\dfrac{r}{z}\right)$$
Now, to put it all together, it's this:
$$(\rho, \theta, \phi) = \begin{cases}
\rho = r^2 + z^2 \\
\theta = \theta \\
\phi = \arctan\left(\dfrac{r}{z}\right)
\end{cases}$$
Spherical to Cylindrical
This is kinda similar to Spherical to Cartesian, but it's much easier. So, let's first convert to $z$ the same way.
$$z = \rho\cos(\phi)$$
We look at the same triangle, and we're able to get r.
$$r = \rho\sin(\phi)$$
$\theta$ is the same, so we're done.
$$(r, \theta, z) = \begin{cases}
r = \rho\sin(\phi) \\
\theta = \theta \\
z = \rho\cos(\phi)
\end{cases}$$
David Witten