Surface Area

Basic Idea

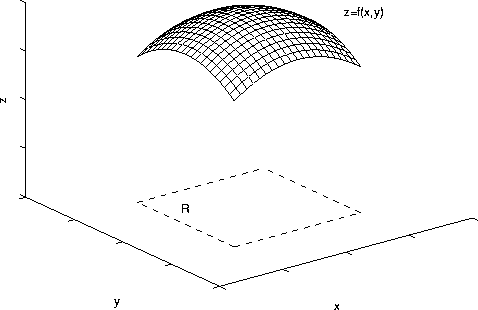
Let's say we want to find the surface area of the curve shown above. We split it up into many boxes, and sum up the areas of each square. Notice that the "squares" aren't actually squares, but as the number of "squares" approaches infinity, that part of the surface becomes essentially flat, and then it's just the area of a square.

Calculate Area

Recall back to the cross product post a while back. The magnitude of the cross product is equal to the area of a parallelogram formed by those two vectors. Now, what are the vectors? Let's say we have this equation $$r(u, v) = < x(u,v), y(u,v), z(u,v)> $$ This doesn't have to be x and y, or r and $\theta$. It can be anything you want. Now, the vectors are the partial derivatives $r_u$ and $r_v$. This is because they are also directional derivatives in perpendicular directions. The directional derivative in the $<1,0>$ direction is $r_u$ and the directional derivative in the $<0,1>$ direction is $r_v$.
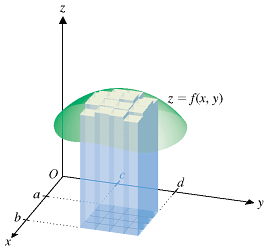
Without being too rigorous, pretty much we're adding up the area (magnitude of the cross products) for each point (x,y). We've seen this before! Double integration! $$\int\int|r_u \times r_v| dx dy$$

Case of z = f(x,y)

This is a common thing to see. We make the vector equal $< x, y, f(x,y)>$. So $r_x$ = $< 1, 0, f_x>$. $r_y$ = $< 0, 1, f_y>$. Taking the cross product gets you $< -f_x, -f_y, 1>$. The magnitude of that is $\sqrt{f_x^2 + f_y^2 + 1}$. The surface area becomes $$\int\int\sqrt{f_x^2 + f_y^2 + 1}dxdy$$

Example

Find the surface area of the surface $r(u,v) = < u\cdot v, u + v, u - v>$, where $u^2 + v^2 \leq 1$.

First, we have to find the partials. $$r_u = < v, 1, 1>$$ $$r_v = < u, 1, -1>$$ $$r_u \times r_v = <-2, u + v, v - u>$$ $$|<-2, u + v, v - u>| = \sqrt{4 + 2u^2 + 2v^2}$$ Notice how we can convert this to polar. We let $u^2 + v^2 = r^2$, and it becomes really easy, because the region is within a circle of radius one. Remember we have to multiply by r first. $$\int_0^{2\pi}\int_0^1r\sqrt{4 + 2r^2}\, d{r} \, d\theta{}$$ Notice how nothing is in terms of theta, so you can turn the outer integral into a scalar $2pi$. Now, we have a one dimensional integral. $$2\pi\int_0^1r\sqrt{4 + 2r^2}\, \mathrm{d}r$$ All you have to do now is a u-substitution, and you get $\boxed{\frac{\pi}{3}(6\sqrt{6} - 8)}$