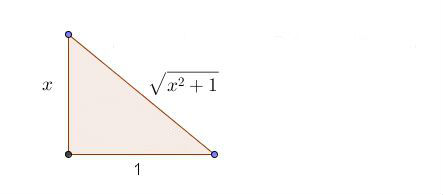Trigonometric Substitution

Let's say you have the integrals $\sqrt{a^2 - u^2}$, $\sqrt{a^2 + u^2}$, and $\sqrt{u^2 - a^2}$. There's a very nice way to solve these, using trigonometric substitution. This is done by constructing a triangle, and setting the expression to a trig function in terms of $\theta$. I'll explain with a few examples.
Note: I doubt this will be on the AP, but it's still a useful method of solving integrals.

Example 1

$$\int\mathrm{\sqrt{9-x^2}}\, \mathrm{d}x$$ $$\text{Now, we can do something cool. Look at the triangle below}$$ $$\text{We can let} \cos{\theta{}} = \frac{\sqrt{9 - x^2}}{3}\text{,so } 3\cos{\theta{}} = \sqrt{9 - x^2}$$ $$\text{We still need a dx, so } x = 3\sin{\theta}, dx = 3\cos{\theta}$$ $$\text{Now, we can make a new integral} \int\mathrm{9\cos^2{\theta{}}}\, \mathrm{d}\theta{}$$ $$\text{Now, we just have to evaluate } \cos^2{\theta{}} = \frac{1}{2} + \frac{\cos{2\theta{}}}{2}$$ $$\frac{9}{2}\int\mathrm{\cos{2\theta{}} + 1}\, \mathrm{d}\theta=\frac{9}{2}(\frac{\sin{2\theta}}{2} + \theta{}) + C=\frac{9}{2}(\sin{\theta{}}\cos{\theta{}} + \theta{}) + C$$ $$=\frac{9}{2}(\frac{x}{3}\frac{\sqrt{9 - x^2}}{3} + \arcsin{\frac{x}{3}}) + C$$ $$=\frac{1}{2}(x\sqrt{9 - x^2} + 9\arcsin{\frac{x}{3}}) + C$$

Example 2

$$\int\mathrm{\frac{1}{(x^2 + 1)^{\frac{3}{2}}}}\, \mathrm{d}x$$ $$\text{First we can rewrite this } \int\mathrm{\frac{dx}{\sqrt{x^2 + 1}^3}}$$ $$\text{By looking at the triangle below, we can see that } \cos{\theta} = \frac{1}{\sqrt{x^2 + 1}}, and \tan{\theta} = x, so \sec^2{\theta} = dx.$$ $$\int\mathrm{\cos^3{\theta}\sec^2{\theta}}\, \mathrm{d}\theta=\int\mathrm{\cos{\theta}}\, \mathrm{d}\theta$$ $$=\sin{\theta} + C = \frac{x}{\sqrt{x^2 + 1}} + C$$

Theta is in the bottom right corner