Double Integration

Single Integration

In single integration, we essentially added all of the y-values for every x-value in a set domain. Back then, the definition of an integral on [a,b] was the limit of a Riemann sum:

$$\lim_{\Delta{}x \to 0}\Sigma{}f(x_i^*)\cdot\Delta{}x_i$$ So, we add a bunch of rectangles. In double integration, we add rectangular prisms.

Inner Partitions

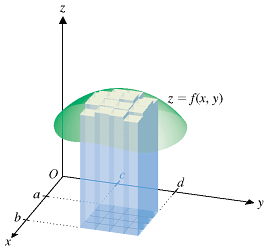
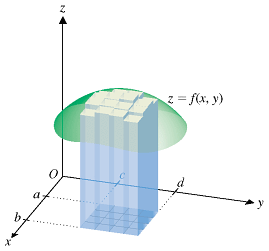
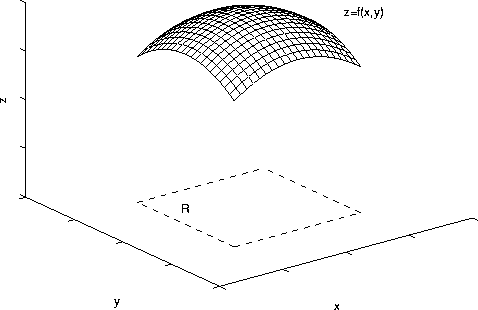
In double integration, we do something where we split a region up into many squares, and we sum up the volumes of the prisms made from the squares. Now, we add up all of the z-values for every square created by the point (x,y).

To actually calculate a double integral, the area of the partitions approaches zero.

Evaluation

Before we start, we have to define the two types of regions. 

Type 1

This is "normal", or at least more familiar. This is when the y's are bound by two functions f(x) and g(x) and the x's are bound between constants.

This is evaluated by doing: $$\int_{a}^{b}\int_{g_1(x)}^{g_2(x)}f(x,y)\,dy\,dx$$ $$= \int_{a}^{b}\left(\int_{g_1(x)}^{g_2(x)}f(x,y)\,dy\right)\,dx$$ The inner integral sets x constant and calculates the area in the y-direction only. This converts it to a single variable function: $\int k(x)\,dx$, where k(x) is the volume of the sliver of some x, and the integral is the sum of all of those slivers equaling the total volume.

Type 2

 This is inverted. This means the x's are bound by two functions f(y) and g(y), and the y's are bound between constants.

This is evaluated by doing: $$\int_{a}^{b}\int_{h_1(y)}^{h_2(y)}f(x,y)\,dx\,dy$$ $$=\int_{a}^{b}\left(\int_{h_1(y)}^{h_2(y)}f(x,y)\,dx\right)\,dy$$ The interpretation is the same as Type 1, just the other way around.

Examples

$$\int_0^1\int_x^1 e^{y^2}\,dy\,dx$$ Here, we can see that y is bound by y = x and y = 1, and x is bound by x = 0 and x = 1. Notice that doing the integral as it is would be impossible. You can't integrate $e^{y^2}$ with respect to y. Now, if you switch the bounds, it can be done. Now, you go from x = 0 to y, and y goes from 0 to 1. $$\int_0^1\int_0^y e^{y^2} \,dx\,dy$$ $$=\int_0^1 e^{y^2}\cdot y \,dy$$ This is just a u sub $$=\dfrac{1}{2}\int_{0^2}^{1^2}e^u \, du = \dfrac{1}{2}(e - 1)$$